NMPC-based control for Quadrotor trajectory tracking with constrained inputs

This work aims to develop a nonlinear model predictive controller to achieve trajectory tracking for a quadrotor subject to input constraints.

Advisor: Dr. Meriem Laleg

Motivation

The objective is to find a control strategy that allows the states of a quadrotor to converge to an arbitrary set of time-varying reference states. Though it is possible to control a quadrotor using linear control techniques by linearizing the system around a trim point even if the quadrotor model is coupled and highly nonlinear, nonlinear control methods are preferred to obtain better performance. Multiple nonlinear methods such as sliding mode, backstepping, adaptive and feedback linearization have been demonstrated to be effective for quadrotor control.

However, none of these control methods take state and control constraints into account, we might face instability issues due to saturation and violation of feasible region. Hence, the nonlinear MPC is proposed to control the quadrotor and handle input constraints at the same time. Also, less effort for tuning is required in MPC structure, since we can simply put weights on states based on the degree of importance. The main drawback of MPC is the computation complexity, because the optimization problem need to be solved iteratively over a whole time period. Thanks to the development of technology, more powerful solvers are available to cope with MPC’s computation demand.

Methodology

In this study, a nonlinear MPC controller is developed to achieve trajectory tracking for a quadrotor subject to input constraints. The optimal control problem (OCP) is transformed into a nonlinear programming problem (NLP) using multiple shooting method, which requires less computational effort and provides higher numerical stability. The IPOPT solver of the open-source optimal tool CasADi is used to solve the nonlinear programming problem in an efficient way. Multiple flight scenarios were performed to show the NMPC address the control problem in high performance.

Github link

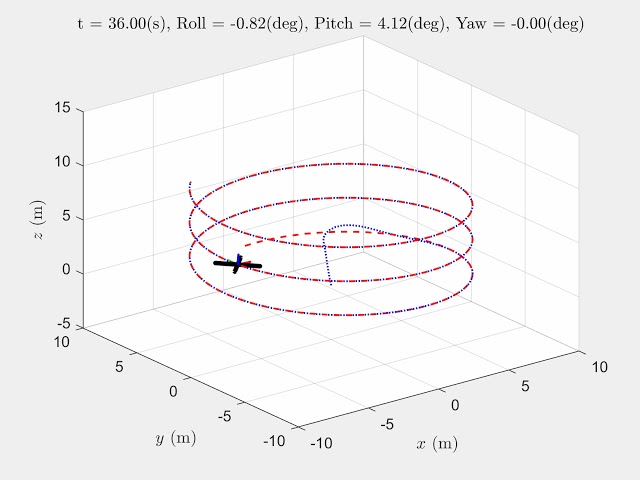
Simulation Results

The figure shows that NMPC has the ability to stabilize the quadrotor on the desired trajectory, and to keep the control inputs in the operation range over a whole time interval simultaneously. In other words, the nonlinear MPC can achieve satisfactory performance and handle constraints, which would be more practicable compared to conventional control methods.

However, the closed-loop of the quadrotor was not guranteed in every desired trajectories. The stability issue involves the initial condition, selection of terminal constraints and length of prediction horizon. Therefore, more systematic stability analysis should be furthered investigated to improve reliability.

Oral Presentation

References

[1] Luukkonen, T., “Modelling and control of quadcopter”, Independent research. project in applied mathematics, Espoo (2011) (link)
[2] Gijs van Lookeren Campagne. A nonlinear model predictive control based evasive manoeuvre assist function.
[3] K. Worthmann, M. W. Mehrez, M. Zanon, G. K. I. Mann, R. G. Gosine, and M. Diehl. Model predictive control of nonholonomic mobile robots without stabilizing constraints and costs. IEEE Transactions on Control Systems Technology, 24(4):1394–1406, 2016. (link)
[4] MPC and MHE implementation in Matlab using Casadi Workshop hosted by Mohamed W. Mehrez